Its been over a month since I last posted here because I’ve been busy with my job and having way too much fun with programming my ascii-rpg (which I will also be doing a blog post about some day). But as you can see I found some time to write part two of how to build a 3D scanner.
Last time I talked about calculating the intersection between a line and plane because those points are needed to reconstruct a 3D model. In that post I said that in order to calculate the intersection point we need to know how a camera projects a point in world space to image space. The projection of this point to image space can be represented by the following equation:
As you can see there are quit a lot of parameters involved in the projection. The vector on the left is the point in image space. The vector on the far right is the point in world space and in the middle are the rotation matrix R and the position vector T inside another matrix. This is the extrinsic matrix which is the position and orientation of the camera in the world. Left to that is the matrix A and this is the matrix that consists of the intrinsic parameters, the ones we are interested in. The equation also contains the scalar s on the far left. This number is a by-product of this projection and is essentially an arbitrary scaling factor needed to balance the equation. It is somewhat related to the depth at which a point in world space lies as seen from the camera.
The intrinsic parameter matrix A consists of the following components:
The αx and αy parameters here are the scaling factors that can be calculated by taking the focal distance and dividing them by the horizontal and vertical size of a pixel on the camera chip. So you expect these numbers to be pretty big (usually around 1000) and that they are roughly the same, because the pixels usually aren’t very rectangular. The u0 and v0 parameters together are the principal point, in pixels. This is the point where the optical axis of the lens intersects with the camera chip. Lastly γ is the skew factor. This is a scalar indicating the degree to which the camera chip looks like a parallelogram. This usually is a very small value.
There are also parameters that affect the projection that can’t be expressed with matrices, because they are non-linear. Among these are the radial distortion parameters, which are the culprits for the fish-eye lens effect that is sometimes seen in photographs. Radial distortion can be described with the following equation:
The parameters k1 and k2 are the distortion parameters and they are also part of the intrinsic parameters. However that’s not what is interesting about this equation. The thing is this equation requires normalized image coordinates which are the x and y parameters. The x and y with the caron sign on top of it are the distorted normalized coordinates. The normalized image coordinates can be calculated by subtracting the corresponding component of the principal point, either u or v, from a image coordinate and dividing it by the corresponding scaling parameter, αx or αy. This normalization is required because radial distortion is applied from the principal point and writing it this way causes the distortion parameters to be independent from the camera chip and to only depend upon the properties of the lens of the camera.
Alright then, so how are we going to calculate all of this? There exists various algorithms for calculating these parameters and most work by giving the algorithm a set of points in world space on an object and a number of sets of those world points projected to image space. The algorithm will then work out which set of camera parameters, both intrinsic and extrinsic, will project the points in world space to image space with the smallest amount of error. The error is calculated by taking a projected point and calculating the distance to the corresponding image point then averaging that for all the point pairs. This is usually called the reprojection error.
A chessboard is usually chosen as a object to generate these points. This is because the corners of the squares of a chessboard are really easy to find in an image with a certain algorithm (I won’t discuss it here but it shouldn’t be too hard to find.) And the points in world space are simply made by measuring a side of a chessboard square. Just take one of corners of the chessboard as the origin of the coordinate system and then they are trivial to calculate.
Writing a algorithm that calculates the camera parameters yourself takes quite a lot of time and effort, but fortunately there already exists an implementation in a open source library. This library is OpenCV and has a great many algorithms related to computer vision, so I made a console application with it that takes a number of images of chessboards and spits out the intrinsic camera parameters. The application can be downloaded at the bottom of this post and also includes a readme because of certain criteria the images must meet.
The application also generates images that show the found points of the chessboards:
To the left is the one of the input images and to the right is image with the chessboard corners marked.
The intrinsic parameters of my crappy webcam are:
αx = 779.336
αy = 792.872
u0 = 341.728
v0 = 265.41
k1 = 0.0223096
k2 = -0.577994
Unfortunately it doesn’t calculate γ so we’ll just have to assume it is zero.
So now that we know the intrinsic parameters we can calculate the mathematical lines that each pixel corresponds to. To do this we must basically apply the projection in reverse, so lets first find a way to remove the distortion from a pixel coordinate. Now coming up with a analytical solution to do this might be a bit hard, in fact multiplying all the variables in the equation until there are no parenthesis left ends up with fith-order polynomial and apparently those are impossible to solve. So we are going to do this with a numeric approximation. Because the distorted coordinates are pretty close to the undistorted coordinates we can use the distorted coordinates instead of the undistorted parameters in the last part of the distortion equation (the part between the brackets). We can get away with this because the normalized coordinates are smaller than one, so squaring them only makes them smaller and have less effect on the result of the equation. Using this, we can rewrite the distortion equation as an undistortion iteration:
Where the i stands for the i-th iteration. At i = 0 the variables with i as a index are equal to their distorted counterparts and at i = ∞ they are equal to their undistorted counterparts. Of course we aren’t going to do an infinite amount of iterations and while testing this iteration I have found that even after 10 iterations the difference between the approximated coordinates and the actual ones is so small that the error is very unlikely to have an effect on anything remotely macroscopic.
Now we can just convert the normalized coordinates to image coordinates by multiplying by the corresponding scaling parameter αx or αy and adding the corresponding component of the principal point u0 or v0. The only thing left is to multiply the image coordinate with the inverse intrinsic parameter matrix to obtain a vector pointing from the center of the camera towards the point in world space that was projected on the image. Don’t forget to normalize the vector.
I also wanted to do a little test to see how well all these equations would work, but that would require a description of the setup and I want to save that for the next post so I will talk about that another time.
CamCalib application: http://www.mediafire.com/?tbd34f2gbxdx4dd




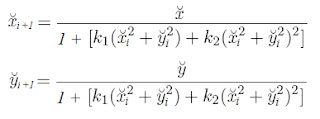
Geen opmerkingen:
Een reactie posten